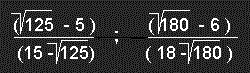|
|
Радзюкевич Андрей Владиславович, старший
преподаватель кафедры КТП
Новосибирской государственной архитектурно-художественной академии |
|
Красивая сказка о “золотом
сечении”.
 |
|
Около 20 лет назад у меня возник интерес к проблеме “золотого сечения” в архитектуре и искусстве...
Изучив достаточно большой объем исследований и исторических
документов по этой теме и сопоставив огромное количество точек
зрения, я пришел к неожиданному для меня выводу, что в этой части
архитектурной науки практически безраздельно господствуют мифы.
Причем, с каждым годом эти мифы приобретают все более красивую и
модную упаковку. Понятие “Золотое сечение” проникло в названия фирм
и престижных конкурсов. В системе автоматизированного проектирования
“Allplan-Allplot” последней версии появился даже инструмент,
позволяющий архитектору в автоматизированном режиме производить
разметку форм проектируемого объекта по пропорциям “золотого
сечения”. Это стало возможным на фоне того, что современные
архитекторы и дизайнеры в абсолютном большинстве своем убеждены в
том, что древние зодчие и мастера всевозможных искусств творили с
помощью “золотого сечения” потому, что оно позволяло создавать более
гармоничные и привлекательные формы. Многие полагают, что
эмпирическое выявление в памятниках архитектуры пропорций, близких к
пропорции “золотого сечения”, дает ключ к раскрытию очень вважного секрета древних мастеров.
Считается, что секрет практически раскрыт и
следует как можно шире использовать “золотую” пропорцию в
современном проектировании. Убежденность дошла до такой степени, что
иные оценки “золотого сечения” воспринимаются многими как
карамольные. Неоднократно обращал внимание на то, что мои
собеседники начинали на меня смотреть как на дядю “с приветом”,
когда я пытался привести те или иные аргументы, ставящие под
сомнение то, что “уже доказано однозначно и многократно”.
На сегодняшний день накопилось так много “доказательств”, что
можно подумать, что “золото” находится буквально везде - в
исторических документах, в пропорциях памятников архитектуры и
искусства, в пропорциях человеческого тела, в основе мироздания и
т.д. и т.п.
На этом общем бодром многоголосом фоне как-то теряются работы
одиночек, пытающих говорить о противоположном. Таким одиночкой был в
свое время В.П.Зубов, имя которого до сих пор известно лишь узкому
кругу специалистов. Как это у нас было принято в порядке вещей,
масштабность и глубина работ В.П.Зубова оказались обратно
пропорциональными их тиражам. Несмотря на то, что роль Зубова в
развитии историко-архитектурной науки была огромной
(Т.Ф.Саваренская), недавнее переиздание основных его работ было
осуществлено микроскопическими тиражами. Так например, феноменальный
труд Зубова “Архитектурная теория Альберти” была издана тиражом
всего в 600 экземпляров. В то же время, книги И.Ш. Шевелева,
убежденного сторонника “золота” были выпущены в свое время
Стройиздатом тиражами в 15 тысяч (1986) и 20 тысяч (1990)
экземпляров. |
|
Если все-таки любознательный читатель попытается разыскать работы
Зубова, то его ждут большие сюрпризы. Лично меня эти работы поразили
тем, что я наконец понял, каким должно быть подлинно научное
исследование по теории и истории архитектуры. Кроме того, приводимая
Зубовым предельно полная научная аргументация по проблеме “золотого
сечения” напрочь убивает всякое желание искать “золото” в документах
по истории архитектуры и в самих памятниках архитектуры.
Большой разрушительный эффект производят также фрагменты чудом
сохранившихся подрядных записок на строительство Арсенала в Пирее и
Эрехтейона в Афинах. Эти тексты предельно просты:
“ Сделать стены вышиной... в двадцать семь футов, а двери вышиной в
пятнадцать с половиной футов. И сверху положить перемычки... длиной
в двенадцать футов...”;
“ Во всех стенах сделать окна ... вышиной в три фута, шириной в два
фута...”;
“ И поставить столбы... толщиной в полтора фута, шириной в три фута
одну пядь и длиной в четыре фута”;
“ Сделать одиннадцать стеновых блоков имеющих длину четыре фута,
ширину два фута и высоту полтора фута...” и так далее и в том же
духе.
|
Как
видим, предельно просты не только тексты, но и размеры
строительных элементов. Эта простота чисел никак не вяжется ни
с иррациональным “золотым сечением”, ни с его целочисленным
заменителем - числами Фиббоначчи. В них нет ничего
таинственного и загадочного. Наоборот, все выглядит как-то
даже скучно и буднично. Неудивительно, поэтому, что
практически никто не пытается найти “золото” в формах Арсенала
в Пиреях, реконструкцию которого сделал еще Огюст Шуази. А вот
в формах Эрехтейона “золото” упорно ищут. Более того,
И.Ш.Шевелев и К.Н.Афанасьев, “нашедшие” в нем “золото”,
приводят в своих списках библиографии источник, содержащий
тексты подрядной записки на строительство Эрехтейона (Paton
J., Stevens G. The Erechteum. Cambridge.1927). При этом,
используя из этого источника обмерные данные по Эрехтейону,
они умудряются никак не увязывать свои “открытия” с
содержанием подрядной записки?!
Что же касается эпохи Возрождения, то весьма показательным
является содержание работ знаменитого итальянского математика
Луки Пачоли (1445-1514гг). В трактате “О божественной
пропорции”, оформленном Леонардо да Винчи, Лука Пачоли дает
приблизительные математические формулы пропорции “золотого
сечения”. В переводе на современные математические символы эти
формулы таковы:
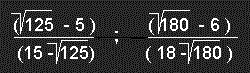
Невозможно даже представить себе, как мог бы зодчий
рассчитывать смету и задавать строителям размеры элементов
сооружений с помощью таких формул. Неудивительно поэтому, что
в трактатах теоретиков эпохи Возрождения, в том числе и в
трактатах и записках Леонардо да Винчи, пропорция "золотого
сечения" не нашла никакого отражения. Что же касается
эстетически предпочтительных пропорций в эпоху Возрождения, то
в качестве характерного примера можно привести рекомендации
Андреа Палладио - выдающегося теоретика и практика
архитектуры. В своем трактате об архитектуре он перечисляет
наиболее предпочтительные пропорции для планов зданий.
Пропорция 5/3, наиболее близкая по значению к "золоту"
приводится только на седьмом месте, уступая таким соотношениям
как 1/1, 3/2, 2/1, 3/1, 4/3, 4/1. Разумеется, Палладио вряд ли
догадывался о том, что пропорция 5/3 близка к "золоту". Об
этом архитекторы начали "догадываться" только в начале 20 века
и начали сознательно его использовать. Именно в это время
впервые и заблестело "золотое сечение" в произведениях
И.Жолтовского и Ле Корбюзье.
|
|
 |
|
|
.
Что касается метода работы зодчих ранних исторических периодов, то
он наиболее точно передан в документе, которому можно придать
обобщающий характер. Речь идет о содержании подрядной записки
Трофима Игнатьева - зодчего Иосифо-Волоколамского монастыря. В ней
сообщается, что при строительстве ворот, их высоту следует выбирать
по принципу: “...а буде покажется высоко и убавить аршин,... а буде
ниско - прибавить аршин же”.
Большое количество аргументов против увлечения “золотым сечением”
в начале 20 века было введено в научный оборот немецким
исследователем Г. Тимердингом. В частности, он ставит под сомнение
результаты работ Цейзига, Пфейфера и Фехнера, исследователей,
которые еще в 19 веке первыми нашли в пропорции “золотого сечения”
необычные свойства. Он также провел большую статистическую работу по
обмерам форматов картин, которые по утверждению Фехнера, в основном,
были близки “золотой” пропорции. Измерив форматы более 700 картин из
19 наиболее богатых шедеврами картинных галерей мира, Тимердинг
отмечает, что наиболее распространенным форматом для “узких” картин
является формат, близкий пропорции 5/4, а для “широких” картин -
3/4.
Еще один устойчивый миф о “золоте” опирается на всеобщее
убеждение о том, что человеческое тело построено по пропорции
“золотого сечения”. Наиболее убедительными и авторитетными по этому
поводу считаются мысли Ле Корбюзье изложенные им в книге “Модулор”.
На основании работы Матилы Гика, который, в свою очередь основывался
на результатах антропометрических исследований Цейзинга, проведенных
еще в 1850 году, Ле Корбюзье в 1947 году разработал систему
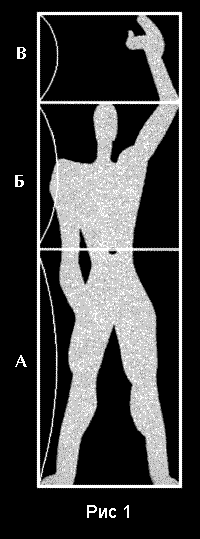
пропорционирования, названную им “Модулором”(рис.1). Система
основана на том предположении, что основные размеры человеческого
тела соотносятся между собой в пропорции “золотого сечения”. В
данном случае, используются три базовых размера:
- высота человека от подошвы до пупка (размер А);
- высота от пупка до макушки (размер Б);
- высота от макушки до кончиков пальцев поднятой вверх руки
(размер В).
|
 |
Абсолютную авторитетность “Модулору” придало положительное
высказывание о нем Альберта Эйнштейна. Он заявил, что “... эта
гамма пропорций, мешающая делать плохо и помогающая делать
хорошо”. Несмотря на то, что Эйнштейн являлся специалистом по
физике, а не по архитектурным пропорциям, его высказывание
воспринималось и воспринимается многими как неоспоримая истина.
Несмотря на такую рекламу, как это ни странно, за прошедшую
половину века “Модулор” так и не получил широкого практического
распространения. Тем не менее, в теоретическом отношении,
“Модулор” по-прежнему считается потенциально ценным. Главное
достоинство “Модулора”, по мнению Ле Корбюзье, заключается в его
антропометричности. С его помощью можно создавать
антропометричные габариты пространства, которые, благодаря своей
“соразмерности” человеку, будут оказывать на него положительное
эстетическое воздействие.
Антропометричность “Модулора” никогда и ни кем не подвергалась
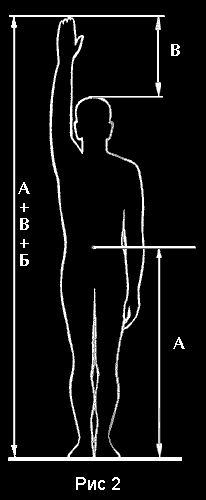
сомнению. В связи с этим, исследовательский интерес представляют
материалы содержащиеся в “Антропометрическом атласе”, выпущенном
ВНИИТЭ еще в 1977 году (рис.2). В нем представлены результаты
широких статистических антропометрических измерений, проведенных
на территории бывшего СССР (РСФСР, Армянская ССР, Литовская
ССР). В результате их проверки появились большие сомнения в
антропометричности “Модулора”. Так, например, по “Модулору”
получается, что высота человека с поднятой рукой ровно в два
раза больше высоты от подошвы до пупка, так как геометрическая
прогрессия “золотого сечения” является аддитивной, т.е. каждый
ее член равен сумме двух предыдущих. По “Антропометрическому
атласу” для различных групп мужчин, эта величина колеблется в
переделах от 2,1225 до 2,144 (в среднем 2,132). Примерно такие
же результаты получаются при анализе данных по различным группам
женщин (от 2,106 до 2,136). Сопоставление других ключевых
размеров и пропорций показали значительные расхождения между
результатами антропометрических измерений и “антропометрическим
модулором” (табл.1). |
|
| |
Размер "А" |
Размер "Б" |
Размер "В" |
Пропорция "А/Б" |
Пропорция "Б/В" |
| "Модупор" для роста в 175
см |
108 см |
67 см |
41 см |
1,612 |
1,634 |
| "Модупор" для роста в 183
см |
113 см |
70 см |
43 см |
1,614 |
1,628 |
| Среднее значение по
"Антропометрическому атласу" для мужчин |
103,13 см |
68,53 см |
48,17 см |
1,505 |
1,423 |
| "Дорифор" Поликлета |
118,5 см |
80,5 см |
--- |
1,472 |
--- |
| "Канон" Леонардо да Винчи |
14,5 пядей |
9,5 пядей |
--- |
1,526 |
--- |
Таблица 1.
|
|
Соотношение размеров А к Б равное 1,505 отличается от “золотого
сечения” на целых 7 процентов. Соотношение же размеров Б к В
разделяет с “золотом” уже более 12 процентов. Такие расхождения
“Модулора” с фактами ставит под сомнение его антропометричность.
Имея фактические значения обмеров, можно отождествить их с
элементарными целочисленными соотношениями. Так, соотношение А к
Б очевидно тожественно простейшему полуторному соотношению. А
отношение Б к В очень близко соотношению 10/7. В целом же
фактические значения тождественны пропорциональной цепочке А/15
= Б/10 = В/7. Данная модель с простейшими числовыми
соотношениями является гораздо более антропометричной, чем
“Модулор” Корбюзье. Геометрическая прогрессия на такой модели
построена быть не может и, следовательно, пропорцию “золотого
сечения” следует искать где-то в другом месте. Может возникнуть
предположение, что обычные антропометрические данные не
показательны для идеальной схемы, а более “правильными” следует
считать пропорции тел, изображенных в великих произведениях
искусства. Для беглой проверки этого предположения возьмем
статую Дорифора (рис.3), автором которой являлся Поликлет,
создатель знаменитого, но неизвестного никому, канона пропорций.
Мною были произведены замеры отливки этой статуи, хранящейся на
кафедре “Рисунка, живописи и скульптуры” НГАХА. Результаты
показали, что его пропорции отклоняются от “золота” в еще
большей степени (табл.1). Расхождения в данном случае составляют
уже более 9 процентов против 7 процентов в случае сопоставления
с антропометрическими данными. Отклонение же пропорций Дорифора
от усредненных соответствующих пропорций современных мужчин
составляет всего 2 процента.
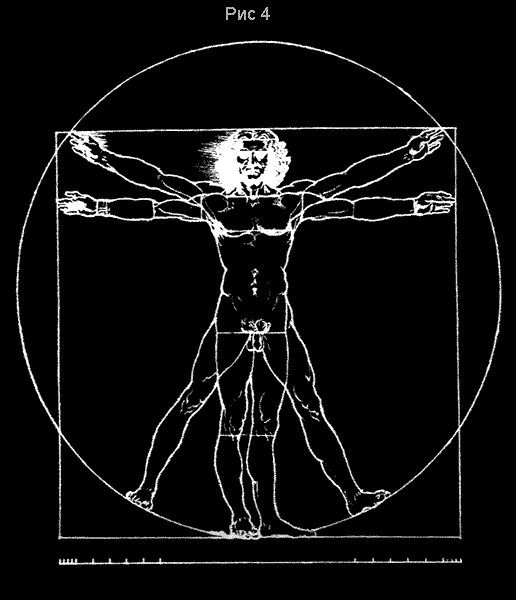
Интерес представляют также пропорции человеческого тела
представленные на рисунке Леонардо да Винчи, хранящемся в
настоящее время в Венецианской академии (рис.4). Используя
масштабную линейку, изображенную в нижней части этого рисунка,
можно определить, что сторона квадрата, в который вписана фигура
человека, равна 24 пядям (6 футов). Диаметр круга схемы равен 29
таким пядям. Поскольку центр круга совпадает с пупком фигуры, то
высота пупка или размер А фигуры равен 14,5 пядям. Размер Б при
этом будет равен 9,5 пядям. Отсюда соотношение А к Б будет равно
1,526 (табл.1). Этот коэффициент также далек от “золотого
сечения”, но также очень близок к данным современных
антропометрических замеров. Следовательно, приведенные
сопоставления показывают, что выбранная Ле Корбюзье система
является формальной схемой, не соответствующей фактическим
антропометрическим данным. Антропометрические измерения
Цейзинга, на которые ссылается Ле Корбюзье, полученные более
полутора веков назад, по всей видимости были проведены на
недостаточно высоком научном уровне. Для поиска “золота” в теле
человека необходимо, прежде всего провести исследования по
выявлению глубинных основ функциональной морфологии. Следует
выяснить, какие именно биологические процессы оптимизируются с
помощью “золотого сечения”? Каков механизм их протекания? Каковы
элементы системы и где их точные границы? Пока не будет научно
обоснованных ответов на этот вопросы, поиски “золота” не выйдут
за рамки предположений и догадок. Даже, так называемый закон
филлотаксиса в растениях, основан только на элементарных
эмпирических наблюдениях. Следует признать, что на сегодня
“золотое сечение” играет роль заманчивой сказки для
научно-популярных и рекламных изданий. У этой сказки красивая
внешняя форма, а внутри пустота. Как в мыльном пузыре.
|
|
 |
|
|
Ответить...
Обсуждения...
Здравствуйте Андрей Владисдавович!
Бархин & Бархин в "Деталь в творчестве Палладио и декоративное убранство церквей Венеции" сообщают, что диаметр абаки Пантеона составляет не 72 части (при нижнем диаметре колонн в 36 частей), а - 77 частей…
Ранее известно:
1. - длина окружности Пантеона - 308 (77 х 4) локтей,
2. - высота алтаря (смотри: "The Temple Of Ezekiel by Lambert Dolphin" (http://www.templemount.org/ezek1c.jpg)) - 19,25 частей (77 x 0,25)...
Кроме того: мера в 7 царских локтей соответствует мере в 11 локтей Гора.
Это обстоятельство свидетельствует об особом её статусе данной меры (гипотетической меры), особом её названии и почитании метрологами Египта (мне оно, к сожалению, не известно), а также о мере в 77 раз меньшей...
Спасибо за внимание, Г.
Уважаемый Андрей Владиславович!
Про гипотезу - почти понятно. Особенно если полагать, что фактов (как таковых!) в природе вроде вовсе и не наблюдается :)...
Одни гипотезы... (поддерживаемые сообществом или же - временно (или безвременно) им отвергаемые)...
Кроме того, совершенно не ясен статус Видения Шимона, как, впрочем, и статус Видения Иезекииля...
Думаю, что "3,5" - в известном смысле - кратно семерке... Но здесь (на мой взгляд) в первую очередь "срабатывает" иконическая трансмутация - "одинадцать!"...
P.S. Локоть Гора А (Horus cubit A) так соотноситя с царским локтем (royal cubits), что диаметр в 1 ЛГ "дает" окружность длиной в 2ЦЛ (11ЛГА = 7 ЦЛ).
http://www.seshat.ch/home/circle.GIF
C уважением,
Геннадий.
 18.01.2011, А.Р. : Уважаемый Геннадий! В той статье была высказана только гипотеза. Как было на самом деле - неизвестно. Тем не менее, полагаю, что число, кратное семерке использовалось для размерения круглых форм на основе дроби 22/7. Уважаемый Андрей Владиславович!
Недавно прочел в "Особенности построения храмов Владимиро-Суздальской Руси методом "по образцу"" о том, что "Мера ПОЯСА ШИМОНА" - 3,5 греко-ионийских футов.
Конструкт "3,5" "встречается" также:
1. - Ezekiel 40-42 - A New House for the LORD
40:5-27 – The outer gates and the outer court. What is the purpose of the wall surrounding the temple? The measurement tool of the visionary guide follows the royal cubit instead of the common cubit and measures approximately 1 and ¾ feet long and so his “rod” is approximately 3 ½ yards (or 10 ½ feet) long.
2. - В описании Змея Кундалини - 3,5 кольца.
3. - При расчете количества кессонов в одном секторе (45 градусов) каждого кесонного ряда...
Думаю, что "посыл" этих конструктов - в "позиционировани" космологически значемых чисел "11", "22", "33"... ..."66", "77"...
Геннадий.
P.S. Мера "Три ПОЯСА ШИМОНА" и Мера "Трость Измерения" - Меры одного "чина".
Золотое сечение - это математическая закономерность. Ни чем не хуже и не лучше других прогрессий. Целое в архитектуре сложнее, чем количественное описание. Изначально архитектурный образ не имеет ни какой численной величины. Размер необходим для удобства строительства. Архитектурный объект может иметь тысячи способов измерения и количественного описания. Для известного золотого сечения необходимым и достаточным является только три числа. В строгом смысле оно никогда не применялось в архитектуре. Более того оно не является единственным случаем равенства соотношения целого и его частей, или единственной аддитивной геометрической прогрессией. Мною решена проблема золотого сечения - теорема о существовании множества аддитивных геометрических прогрессий (множества золотых сечений). О чем упоминалось в ранней моей статье "Мифологическое значение золотого сечения и мера его ценности в архитектурной композиции". Древние мифы олицетворения приобретают со временем рациональный по форме миф.
Винокуров Ю.М. - автор концепции персоналистического символизма в архитектуре и развития всей человеческой культуры.
Андрей Владиславович!
Вы пишите, что колонны Пантеона (по их нижнему диаметру) характеризуются следующими величинами:
1. - длина ствола колонна - 8 (64/8),
2. - высота базы - 1/2 (4/8),
3. - высота капители - 9/8,
4. - верхний диаметр ствола колонны - 7/8...
Сложив первые три модуля получаем - 77/8... или 77/7 (по верхн. диаметру ствола колонны)... Отсюда "вырисовывается" число "11": общая высота колонн Пантеона составляет 11-ть модулей типа "верхний диаметр ствола колонны"...
По 11-ть локтей длины окружности приходится на каждый из 28-ми её секторов...
Иначе: модуль колонн Пантеона и модуль его деления на сектора - един.
Спасибо за внимание.
Геннадий.
Здравствуйте Андрей Владиславович!
The Pantheon in Rome. Contributions
Gerd Graßhoff and Michael Heinzelmann and Markus Wäfler, The Pantheon in Rome. Contributions to the Conference Bern, November 9-12, 2006, Bern: Bern Studies 2009
The Bern Digital Pantheon Project was officially launched at an international conference that was held in November 2006 on the first anniversary of the new Institute of Archaeology. Forty leading Pantheon experts accepted the invitation to come together in the Swiss capital. Archaeologists, architectural historians, art historians, historians and engineers were thus able to present and discuss new observations in an exceptionally open and stimulating atmosphere. The conference resulted in an exciting reappraisal of hitherto accepted information, presented new approaches and laid new foundations on which further Pantheon research will be built. This volume documents, therefore, the current state of research on the Pantheon.
Table of Contents
Heiner Knell Das Pantheon in Rom und die Sprache seiner Architektur 11-26 PDF
Pieter Broucke The First Pantheon: Architecture and Meaning (abstract) 27-28 PDF
Adam Ziolkowski What did Agrippa’s Pantheon look like? New Answers to an Old Question 29-40 PDF
Andreas Grüner Das Pantheon des Agrippa: Architektonische Form und urbaner Kontext 41-68 PDF
Mark Wilson Jones The Pantheon and the Phasing of its Construction 69-88 PDF
Gerd Heene Die Kompromisse in der Architektur — Anbau Nord / Anbau Süd: Wie kamen sie zustande? 89-98 PDF
Giangiacomo Martines The Structure of the Dome 99-106 PDF
Lise Hetland Zur Datierung des Pantheon 107-116 PDF
Lynn C. Lancaster Materials and Construction of the Pantheon in Relation to the Developments in Vaulting in Antiquity 117-126 PDF
Allan Ceen The Urban Setting of the Pantheon 127-138 PDF
Wolfram Martini Das Pantheon Hadrians? 139-144 PDF
Tod A. Marder The Pantheon after Antiquity 145-154 PDF
Louise Rice Pope Urban VIII and the Pantheon Portico (abstract) 155-156 PDF
Susanna Pasquali L’attico del Pantheon. Nuovi documenti sui marmi e sulla controversa ricostruzione del 1757 157-170 PDF
Lothar Haselberger The Pantheon: Nagging Questions to No End 171-186 PDF
Nikolaos Theocharis How the Bern Digital Pantheon model can help answer »nagging questions« about the Pantheon 187-194 PDF
Volker Hoffmann The Repaired Columns of the Pantheon(abstract) 195-200 PDF
Paola Virgili Scavi in piazza della Rotonda e sulla fronte del Pantheon 201-214 PDF
Michael Scherer A Sustainable Geodetic Network for Documenting and Monitoring the Pantheon 215-222 PDF
Graziano Mario Valenti A Computing Model for the Pantheon’s Cupola: From the Discrete to the Continuous. The Ideal Continuous Model 223-232 PDF
Thomas Vogel A Structural Evaluation of the Pantheon — Envisaged Tasks 233-242 PDF
Bernd Kulawik The Technical Session 243-246 PDF
Dieses Buch bei buch.de bestellen.
Такой вот сборничек обнаружился... Цифры на чертежах хорошо различимы...
С уважением, Геннадий.
 22.11.2010, : Спасибо, Геннадий! Все обязательно посмотрю... Здравствуйте Андрей Владиславович!
THE MODULAR COMPOSITION OF ROMAN WATER-WHEELS
T. KURENT
Faculty of Architecture, Ljubljana, Cojzova 5, Yugoslavia
Volume 10, Issue 1, pages 29–34, June 1967
The diameter of the Pantheon dome is 43.5 m or in Roman units 147 pedes...
В предисловии к «Тайной Доктрине» Е. Блаватская пишет:
"Все притчи и легенды Библии «нанизаны» на константу 147".
Цитировано: А.Кисель "Кладезь бездны".
Конструкт 147 можно найти и у А. Корнеева. «ТЕТРАКТИС. НОВЫЙ И СПИРАЛЬНЫЙ».
Кроме того:
http://baza.md/uploads/1912081546.jpg
С уважением,
Геннадий.
Здравствуйте Андрей Владиславович!
Прогуливаясь по ул. Голубки легкоо увидеть двух дельфинов семьи Юлиев:
http://www.chronologia.org/dcforum/DCForumID2/11501.html
Похоже, что это остатки южного портика Пантеона.
Геннадий. Андрей Владиславович!
Прошу прощения за описку. Очень торопился. Закрывалась библиотека.
The role of the sun in the Pantheon's design and meaning
Authors: Robert Hannah, Giulio Magli
http://arxiv.org/abs/0910.0128v1
[PDF] From Giza to the Pantheon: astronomy as a key to the architectural...
21 апреля в Пантеоне (день рождения Рима)...
====
Франц Гнедингер выставляет работы по египетским мерам на форуме: http://mathforum.org/kb/search!execute.jspa?userID=410857&forceEmptySearch=true
В этой статье о стоительстве Пантеона (в средние века):
Das Pantheon als neulateinisches Bauwerk
von Christoph Pfister
На сегодня, пожалуй, все.
Геннадий. Здравствуйте Андрей Вячеславович!
Искал так: Google - Картинки - "Alberti Pantheon"...
Домашний адрес страницы: http://www.seshat.ch/home/homepage.htm
Альберти заявлен здесь: http://www.seshat.ch/home/alberti.htm
Leon Battista Alberti, Hypnerotomachia Poliphili / © 2003/2005 Gerhard Goebel und Franz Gnaedinger, fgn(a)bluemail.ch, fg(a)seshat.ch, www.seshat.ch / Designed for Explorer 5 and 6 / Lauftext: Times New Roman 12, GROSSBUCHSTABEN 11, Anmerkungen 11. Mathematische Zeilen: Courier New 11. Vorspann und Links: Century Gothic 12
Получается, что авторы: Gerhard Goebel и Franz Gnaedinger...
Ещё одна интересная работа:
http://www.google.com.ua/imgres?imgurl=http://www.informaworld.com/ampp/image%3Fpath%3D/713703437/906423951/rjar_a_357554_o_f0010g.jpeg&imgrefurl=http://www.informaworld.com/smpp/336643096-10171298/section%25253Fcontent%25253Da906423951%252526fulltext%25253D713240928&usg=__-_89U7Q9M_s45xwTNFUrKX4nlf4=&h=1050&w=1400&sz=329&hl=ru&start=104&zoom=1&tbnid=tlWvDGAQRR49VM:&tbnh=113&tbnw=150&prev=/images%3Fq%3DPiranesi%2BPantheon%26start%3D100%26um%3D1%26hl%3Dru%26sa%3DN%26tbs%3Disch:1&um=1&itbs=1
A geometrical analysis of multiple viewpoint perspective in the work of Giovanni Battista Piranesi: an application of geometric restitution of perspective
Author: Joanna Barbara Rapp
Спасибо за ответ.
Геннадий.
Спасибо, Геннадий, за очень интересную ссылку! Было бы интересно узнать, кто автор реконструкции плана Пантеона... Здравствуйте Андрей Вячеславович.
http://chronologia.org/dcforum/DCForumID2/11501.html#16
Здесь один из планов римского Пантеона и один из планов CASTEL DEL MONTE. Симметрия замка весьма напоминает симметрию Пантеона. И диаметры сооружений – сопоставимы.
Новость о «золотом» сечении в расшифрованном завещании Леонардо да Винчи на нашем сайте: www.istina-fi.ryazan.ru
cтраницы обсуждения
1 2 3 4 5 6 7 8 9 10 >>

 (с) 2002-2024 СибДИЗАЙН.ру
(с) 2002-2024 СибДИЗАЙН.ру
|

|