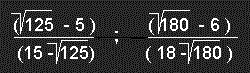|
|
Радзюкевич Андрей Владиславович, старший
преподаватель кафедры КТП
Новосибирской государственной архитектурно-художественной академии |
|
Красивая сказка о “золотом
сечении”.
 |
|
Около 20 лет назад у меня возник интерес к проблеме “золотого сечения” в архитектуре и искусстве...
Изучив достаточно большой объем исследований и исторических
документов по этой теме и сопоставив огромное количество точек
зрения, я пришел к неожиданному для меня выводу, что в этой части
архитектурной науки практически безраздельно господствуют мифы.
Причем, с каждым годом эти мифы приобретают все более красивую и
модную упаковку. Понятие “Золотое сечение” проникло в названия фирм
и престижных конкурсов. В системе автоматизированного проектирования
“Allplan-Allplot” последней версии появился даже инструмент,
позволяющий архитектору в автоматизированном режиме производить
разметку форм проектируемого объекта по пропорциям “золотого
сечения”. Это стало возможным на фоне того, что современные
архитекторы и дизайнеры в абсолютном большинстве своем убеждены в
том, что древние зодчие и мастера всевозможных искусств творили с
помощью “золотого сечения” потому, что оно позволяло создавать более
гармоничные и привлекательные формы. Многие полагают, что
эмпирическое выявление в памятниках архитектуры пропорций, близких к
пропорции “золотого сечения”, дает ключ к раскрытию очень вважного секрета древних мастеров.
Считается, что секрет практически раскрыт и
следует как можно шире использовать “золотую” пропорцию в
современном проектировании. Убежденность дошла до такой степени, что
иные оценки “золотого сечения” воспринимаются многими как
карамольные. Неоднократно обращал внимание на то, что мои
собеседники начинали на меня смотреть как на дядю “с приветом”,
когда я пытался привести те или иные аргументы, ставящие под
сомнение то, что “уже доказано однозначно и многократно”.
На сегодняшний день накопилось так много “доказательств”, что
можно подумать, что “золото” находится буквально везде - в
исторических документах, в пропорциях памятников архитектуры и
искусства, в пропорциях человеческого тела, в основе мироздания и
т.д. и т.п.
На этом общем бодром многоголосом фоне как-то теряются работы
одиночек, пытающих говорить о противоположном. Таким одиночкой был в
свое время В.П.Зубов, имя которого до сих пор известно лишь узкому
кругу специалистов. Как это у нас было принято в порядке вещей,
масштабность и глубина работ В.П.Зубова оказались обратно
пропорциональными их тиражам. Несмотря на то, что роль Зубова в
развитии историко-архитектурной науки была огромной
(Т.Ф.Саваренская), недавнее переиздание основных его работ было
осуществлено микроскопическими тиражами. Так например, феноменальный
труд Зубова “Архитектурная теория Альберти” была издана тиражом
всего в 600 экземпляров. В то же время, книги И.Ш. Шевелева,
убежденного сторонника “золота” были выпущены в свое время
Стройиздатом тиражами в 15 тысяч (1986) и 20 тысяч (1990)
экземпляров. |
|
Если все-таки любознательный читатель попытается разыскать работы
Зубова, то его ждут большие сюрпризы. Лично меня эти работы поразили
тем, что я наконец понял, каким должно быть подлинно научное
исследование по теории и истории архитектуры. Кроме того, приводимая
Зубовым предельно полная научная аргументация по проблеме “золотого
сечения” напрочь убивает всякое желание искать “золото” в документах
по истории архитектуры и в самих памятниках архитектуры.
Большой разрушительный эффект производят также фрагменты чудом
сохранившихся подрядных записок на строительство Арсенала в Пирее и
Эрехтейона в Афинах. Эти тексты предельно просты:
“ Сделать стены вышиной... в двадцать семь футов, а двери вышиной в
пятнадцать с половиной футов. И сверху положить перемычки... длиной
в двенадцать футов...”;
“ Во всех стенах сделать окна ... вышиной в три фута, шириной в два
фута...”;
“ И поставить столбы... толщиной в полтора фута, шириной в три фута
одну пядь и длиной в четыре фута”;
“ Сделать одиннадцать стеновых блоков имеющих длину четыре фута,
ширину два фута и высоту полтора фута...” и так далее и в том же
духе.
|
Как
видим, предельно просты не только тексты, но и размеры
строительных элементов. Эта простота чисел никак не вяжется ни
с иррациональным “золотым сечением”, ни с его целочисленным
заменителем - числами Фиббоначчи. В них нет ничего
таинственного и загадочного. Наоборот, все выглядит как-то
даже скучно и буднично. Неудивительно, поэтому, что
практически никто не пытается найти “золото” в формах Арсенала
в Пиреях, реконструкцию которого сделал еще Огюст Шуази. А вот
в формах Эрехтейона “золото” упорно ищут. Более того,
И.Ш.Шевелев и К.Н.Афанасьев, “нашедшие” в нем “золото”,
приводят в своих списках библиографии источник, содержащий
тексты подрядной записки на строительство Эрехтейона (Paton
J., Stevens G. The Erechteum. Cambridge.1927). При этом,
используя из этого источника обмерные данные по Эрехтейону,
они умудряются никак не увязывать свои “открытия” с
содержанием подрядной записки?!
Что же касается эпохи Возрождения, то весьма показательным
является содержание работ знаменитого итальянского математика
Луки Пачоли (1445-1514гг). В трактате “О божественной
пропорции”, оформленном Леонардо да Винчи, Лука Пачоли дает
приблизительные математические формулы пропорции “золотого
сечения”. В переводе на современные математические символы эти
формулы таковы:
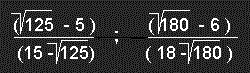
Невозможно даже представить себе, как мог бы зодчий
рассчитывать смету и задавать строителям размеры элементов
сооружений с помощью таких формул. Неудивительно поэтому, что
в трактатах теоретиков эпохи Возрождения, в том числе и в
трактатах и записках Леонардо да Винчи, пропорция "золотого
сечения" не нашла никакого отражения. Что же касается
эстетически предпочтительных пропорций в эпоху Возрождения, то
в качестве характерного примера можно привести рекомендации
Андреа Палладио - выдающегося теоретика и практика
архитектуры. В своем трактате об архитектуре он перечисляет
наиболее предпочтительные пропорции для планов зданий.
Пропорция 5/3, наиболее близкая по значению к "золоту"
приводится только на седьмом месте, уступая таким соотношениям
как 1/1, 3/2, 2/1, 3/1, 4/3, 4/1. Разумеется, Палладио вряд ли
догадывался о том, что пропорция 5/3 близка к "золоту". Об
этом архитекторы начали "догадываться" только в начале 20 века
и начали сознательно его использовать. Именно в это время
впервые и заблестело "золотое сечение" в произведениях
И.Жолтовского и Ле Корбюзье.
|
|
 |
|
|
.
Что касается метода работы зодчих ранних исторических периодов, то
он наиболее точно передан в документе, которому можно придать
обобщающий характер. Речь идет о содержании подрядной записки
Трофима Игнатьева - зодчего Иосифо-Волоколамского монастыря. В ней
сообщается, что при строительстве ворот, их высоту следует выбирать
по принципу: “...а буде покажется высоко и убавить аршин,... а буде
ниско - прибавить аршин же”.
Большое количество аргументов против увлечения “золотым сечением”
в начале 20 века было введено в научный оборот немецким
исследователем Г. Тимердингом. В частности, он ставит под сомнение
результаты работ Цейзига, Пфейфера и Фехнера, исследователей,
которые еще в 19 веке первыми нашли в пропорции “золотого сечения”
необычные свойства. Он также провел большую статистическую работу по
обмерам форматов картин, которые по утверждению Фехнера, в основном,
были близки “золотой” пропорции. Измерив форматы более 700 картин из
19 наиболее богатых шедеврами картинных галерей мира, Тимердинг
отмечает, что наиболее распространенным форматом для “узких” картин
является формат, близкий пропорции 5/4, а для “широких” картин -
3/4.
Еще один устойчивый миф о “золоте” опирается на всеобщее
убеждение о том, что человеческое тело построено по пропорции
“золотого сечения”. Наиболее убедительными и авторитетными по этому
поводу считаются мысли Ле Корбюзье изложенные им в книге “Модулор”.
На основании работы Матилы Гика, который, в свою очередь основывался
на результатах антропометрических исследований Цейзинга, проведенных
еще в 1850 году, Ле Корбюзье в 1947 году разработал систему
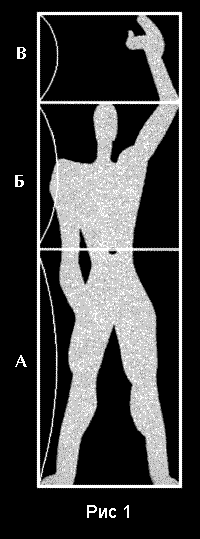
пропорционирования, названную им “Модулором”(рис.1). Система
основана на том предположении, что основные размеры человеческого
тела соотносятся между собой в пропорции “золотого сечения”. В
данном случае, используются три базовых размера:
- высота человека от подошвы до пупка (размер А);
- высота от пупка до макушки (размер Б);
- высота от макушки до кончиков пальцев поднятой вверх руки
(размер В).
|
 |
Абсолютную авторитетность “Модулору” придало положительное
высказывание о нем Альберта Эйнштейна. Он заявил, что “... эта
гамма пропорций, мешающая делать плохо и помогающая делать
хорошо”. Несмотря на то, что Эйнштейн являлся специалистом по
физике, а не по архитектурным пропорциям, его высказывание
воспринималось и воспринимается многими как неоспоримая истина.
Несмотря на такую рекламу, как это ни странно, за прошедшую
половину века “Модулор” так и не получил широкого практического
распространения. Тем не менее, в теоретическом отношении,
“Модулор” по-прежнему считается потенциально ценным. Главное
достоинство “Модулора”, по мнению Ле Корбюзье, заключается в его
антропометричности. С его помощью можно создавать
антропометричные габариты пространства, которые, благодаря своей
“соразмерности” человеку, будут оказывать на него положительное
эстетическое воздействие.
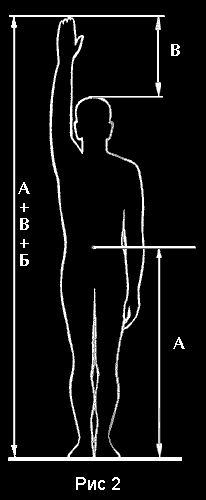
Антропометричность “Модулора” никогда и ни кем не подвергалась
сомнению. В связи с этим, исследовательский интерес представляют
материалы содержащиеся в “Антропометрическом атласе”, выпущенном
ВНИИТЭ еще в 1977 году (рис.2). В нем представлены результаты
широких статистических антропометрических измерений, проведенных
на территории бывшего СССР (РСФСР, Армянская ССР, Литовская
ССР). В результате их проверки появились большие сомнения в
антропометричности “Модулора”. Так, например, по “Модулору”
получается, что высота человека с поднятой рукой ровно в два
раза больше высоты от подошвы до пупка, так как геометрическая
прогрессия “золотого сечения” является аддитивной, т.е. каждый
ее член равен сумме двух предыдущих. По “Антропометрическому
атласу” для различных групп мужчин, эта величина колеблется в
переделах от 2,1225 до 2,144 (в среднем 2,132). Примерно такие
же результаты получаются при анализе данных по различным группам
женщин (от 2,106 до 2,136). Сопоставление других ключевых
размеров и пропорций показали значительные расхождения между
результатами антропометрических измерений и “антропометрическим
модулором” (табл.1). |
|
| |
Размер "А" |
Размер "Б" |
Размер "В" |
Пропорция "А/Б" |
Пропорция "Б/В" |
| "Модупор" для роста в 175
см |
108 см |
67 см |
41 см |
1,612 |
1,634 |
| "Модупор" для роста в 183
см |
113 см |
70 см |
43 см |
1,614 |
1,628 |
| Среднее значение по
"Антропометрическому атласу" для мужчин |
103,13 см |
68,53 см |
48,17 см |
1,505 |
1,423 |
| "Дорифор" Поликлета |
118,5 см |
80,5 см |
--- |
1,472 |
--- |
| "Канон" Леонардо да Винчи |
14,5 пядей |
9,5 пядей |
--- |
1,526 |
--- |
Таблица 1.
|
|
Соотношение размеров А к Б равное 1,505 отличается от “золотого
сечения” на целых 7 процентов. Соотношение же размеров Б к В
разделяет с “золотом” уже более 12 процентов. Такие расхождения
“Модулора” с фактами ставит под сомнение его антропометричность.
Имея фактические значения обмеров, можно отождествить их с
элементарными целочисленными соотношениями. Так, соотношение А к
Б очевидно тожественно простейшему полуторному соотношению. А
отношение Б к В очень близко соотношению 10/7. В целом же
фактические значения тождественны пропорциональной цепочке А/15
= Б/10 = В/7. Данная модель с простейшими числовыми
соотношениями является гораздо более антропометричной, чем
“Модулор” Корбюзье. Геометрическая прогрессия на такой модели
построена быть не может и, следовательно, пропорцию “золотого
сечения” следует искать где-то в другом месте. Может возникнуть
предположение, что обычные антропометрические данные не
показательны для идеальной схемы, а более “правильными” следует
считать пропорции тел, изображенных в великих произведениях
искусства. Для беглой проверки этого предположения возьмем
статую Дорифора (рис.3), автором которой являлся Поликлет,
создатель знаменитого, но неизвестного никому, канона пропорций.
Мною были произведены замеры отливки этой статуи, хранящейся на
кафедре “Рисунка, живописи и скульптуры” НГАХА. Результаты
показали, что его пропорции отклоняются от “золота” в еще
большей степени (табл.1). Расхождения в данном случае составляют
уже более 9 процентов против 7 процентов в случае сопоставления
с антропометрическими данными. Отклонение же пропорций Дорифора
от усредненных соответствующих пропорций современных мужчин
составляет всего 2 процента.
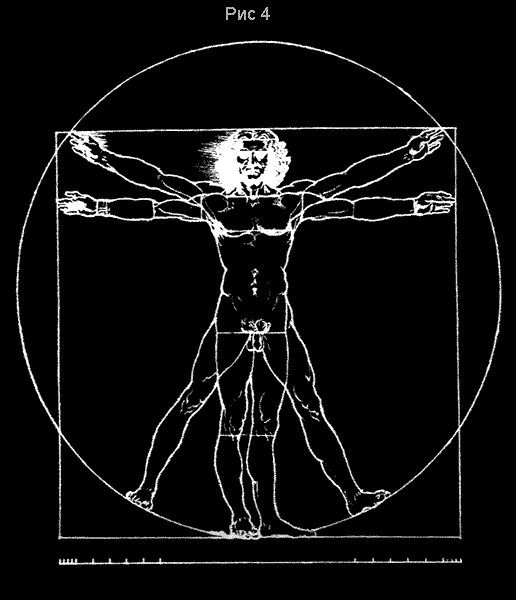
Интерес представляют также пропорции человеческого тела
представленные на рисунке Леонардо да Винчи, хранящемся в
настоящее время в Венецианской академии (рис.4). Используя
масштабную линейку, изображенную в нижней части этого рисунка,
можно определить, что сторона квадрата, в который вписана фигура
человека, равна 24 пядям (6 футов). Диаметр круга схемы равен 29
таким пядям. Поскольку центр круга совпадает с пупком фигуры, то
высота пупка или размер А фигуры равен 14,5 пядям. Размер Б при
этом будет равен 9,5 пядям. Отсюда соотношение А к Б будет равно
1,526 (табл.1). Этот коэффициент также далек от “золотого
сечения”, но также очень близок к данным современных
антропометрических замеров. Следовательно, приведенные
сопоставления показывают, что выбранная Ле Корбюзье система
является формальной схемой, не соответствующей фактическим
антропометрическим данным. Антропометрические измерения
Цейзинга, на которые ссылается Ле Корбюзье, полученные более
полутора веков назад, по всей видимости были проведены на
недостаточно высоком научном уровне. Для поиска “золота” в теле
человека необходимо, прежде всего провести исследования по
выявлению глубинных основ функциональной морфологии. Следует
выяснить, какие именно биологические процессы оптимизируются с
помощью “золотого сечения”? Каков механизм их протекания? Каковы
элементы системы и где их точные границы? Пока не будет научно
обоснованных ответов на этот вопросы, поиски “золота” не выйдут
за рамки предположений и догадок. Даже, так называемый закон
филлотаксиса в растениях, основан только на элементарных
эмпирических наблюдениях. Следует признать, что на сегодня
“золотое сечение” играет роль заманчивой сказки для
научно-популярных и рекламных изданий. У этой сказки красивая
внешняя форма, а внутри пустота. Как в мыльном пузыре.
|
|
 |
|
|
Ответить...
Обсуждения...
 13.02.2013, : уже сейчас вы можете вы можете забить в яндексе о леонардо да винчи и первое что вылезет будет говорить о том что он пичастен к этому
хотя на этот щет есть и другие варианты , утверждать что золотоесечение это миф слишком Андрей Владиславович, к Вашим двадцати лет изучения проблемы золотого сечения добавилось еще более десяти лет опубликования статьи «Красивая сказка о золотом сечении». У Вас не поменялось мнение по данному вопросу? Еще один вопрос. Вы в свое время не отреагировали на мою фразу от 01.02.2009 г. Может быть Вы сейчас попробуете обратить на это внимание.
«К сожалению, никто в своих дискуссиях не обратил внимание на замечание с моей стороны по поводу того, что всем нам известный штрих-код создан по принципу золотого сечения. Если отрицание ЗС в искусстве происходит очень бурно, по причинам либо «недоказанности» или для того, чтобы войти в историю («здесь был Вася»), то по штрих-коду… тишина. Да, это не искусство. Но многие категорически отрицают принцип золотого сечения. А здесь он на первом месте. Звенит! Работает! И что бы там ни говорили, ни писали, ни отрицали критики со званиями или без званий, бумага все стерпит. А слон из басни Крылова продолжает свое шествие, не обращая внимание на посторонний шум и гам!»
С уважением Никитин Сергей.
 16.12.2012, А.Ралзюкевич : Уважаемый Витя! Приведите документальные доказательства, подтверждающие Ваше высказывание.. в своем тексте вы упомянули что леонардо да винчи не имел отношения к золотому сечению но все картины которые он написал созданы по принципу золотого сечения, он усовершенствовал арбалет по принципу золотого сечения. а также золотое сечение привлекает внимания человека. Многие машины созданы по принципу золотого сечения и они разлетаются бешеным тиражом. Что вы скажете на это? Уважаемый Андрей Владиславович, Ваш критицизм по отношению к "золотому сечению" мне очень по душе, но из-за нехватка места не могу распространяться. У меня вопрос: если Евклид употребляет выражение "деление в крайнем и среднем отношении", то это предпоставляет, что имеется некое деление отрезка "в среднем отношении", а также и в "крайнем отношении", и в известном нам специальном случае они совпадают. Так я и срашивяю: встречаются ли у Евклида или где-нибудь в древне-греческой геометрии "средние отношения", не будучи "крайними", либо "крайние отношения", не будучи "средними"? И в итоге, с какой стати именно деление "меньшая часть к большей, как большая к целому" названо "делением в среднем и крайнем отношении"? Я спрашиваю туда и сюда, но не получай вразумительного ответа. Для меня объяснение, что, мол, В является одновременно "средним" в пропорции А:В=В:С и "крайним" в пропорции В:С=А:В, неубедительно, поскольку такое совпадение верно для любого среднего геометрического. А у Евклида рассматривается тот специальный случай, в котором С=А+В. Буду рад Вашему ответу!  19.05.2012, А.Радзюкевич : Мне такие объекты не знакомы... Андрей Владиславович! Дамы и господа! Убедительная просьба подскажите какие здания ( фрагментах) г.Новосибирска используется принцип золотого сечения Три ряда пропорций и три типа прямоугольников (по состоян. на 17.11.11.):
а. 1/2, 2/3, 3/4, 4/5... (1х2, 2х3, 3х4, 4х5...)
б. 1/2х2, 2х2/3х3, 3х3/4х4, 4х4/5х5... (1х4, 4Х9, 9х16, 16х25...)
в. 1/√2, √2/√3 (= 9/11)... (1х√2, √2х√3 (= √6)...)
Касательно прямоугольника √2х√3 интересен казус рационализации: 9 М х 11 М (площаь равна 99 квадр. модулям).
"MATHESIS of Giza Plateau by David Bowman"
http://www.aiwaz.net/uploads/gallery/432.gif
http://www.aiwaz.net/uploads/gallery/431.gif
Геннадий.
В предложении "Модуль стилобата фриза – 25 (5х5) триглифов" слово "фриза" - лишнее. Слово "триглифов" - следует заменить словом "футов".
Андрей Владиславович! Дамы и господа!
Music in pictures (Pythagoras and Alberti)
Автор не указан
«These intervalproportions are fundamental to renaissance-architecture. A nice example is the by Alberti designed cathedral Tempio Malatestiano in Rimini, Italy. In figure 2 you will see the proportions of Pythagoras (based on the Roman foot of 29,6 cm)».
Модуль – 4 (2х2) римских фута. Прямоугольник 25 М х 36 М.
===
===
К вопросу о метрологии и пропорциях русских храмов 16-17 вв.
Радзюкевич А.В.
«Используя размер византийского локтя (0,477м) в качестве модуля, попытаемся сделать реконструкцию проектных размеров башни».
Модуль – 1 (1х1) византийский локоть. Прямоугольник «А» – 9 М х 16 М и прямоугольник «Б» – 16 М х 25 М.
===
===
Парфенон («с мира по нитке»)
Модуль фриза – 9 (3х3) триглифов (размер метопа составляет 1,5 триглифа). 4 М х 9 М.
Модуль стилобата фриза – 25 (5х5) триглифов. Прямоугольник 4 М х 9 М.
==========
==========
Модули Парфенона «заданы» квадратными числами – «9» и «25».
Модуль Tempio Malatestiano – «задан» квадратным числом «4».
Модуль Водовзводной башни – также «задан» квадратным числом – числом «1».
== ==
== ==
Любое квадратное число "n" легко представить как сумму последовательных нечетных чисел – 1 + 3 + … + 2n – 1.
Такая запись (визуально) весьма "напоминает" запись чисел в Древнем Египте.
Геннадий. Продолжу... (Конструкт "30")
Cesare di Lorenzo Cesariano в 1521 году в квадрате 30 Х 30 (900) представил одного из "людей Витрувия".
Над ним - "зонтик"... "О 30-ти спицах"... Здравствуйте Андрей Владиславович!
Продолжу "О конструкте "30"":
11. - 30 "камешков вертикальных" и 30 "камешков горизонтальных" (с шипиками (для сцепления с вертикальными...)),
12. - 30 поясов Шимона (длина (и вариант высоты) Успенского храма в Киеве),
12-а - 30 000 кубич. поясов Шимона (30 х 20 х 50) - виртуальный объём Успенского храма.
С уважением,
Геннадий. Здравствуйте Андрей Владиславович!
Продолжу "Немного о числе "30"":
10. - 30 - колич. тычков прих. на сектор Георгиевской колокольни (общий периметр - 150 тычков (75 ложков).
Отсюда ясно видны след. параллели:
1. 30 больших секторов и 150 (30 х 5) малых в кругах Дж. Бруно
Френсис Гейтс «Искусство памяти»
Глава 9
Джордано Бруно: секрет "Теней"
2. Число "30" неразрывно "связывает" Георгиевскую колокольню с двумя Платоновыми телами - додекаэдром (30 ребер) и икосаэдром (тоже - 30 ребер), которые, в свою очередь, соотносятся с Огнем и Землей (Большими Ян и Инь).
"Геометрия жизни. Влияние формы упаковки на человека и пространство"
http://www.upakovano.ru/pictures/article_imgs/Other_magazines/packaging_rd/3_big.jpg
Спасибо за внимание.
Геннадий.
Здравствуйте!
Немного о числе "30":
1. - 30 - число курий в Др. Риме
2. - 30 - колич. серебрянников
3. - 30 - сумма числ. значений фигур Пифагорейского Кватернера
4. - 30 - периметр и площадь треугольника 5-12-13
5. - 30 - 1 / 28 800 диаметра Солнца а милях (864 000 миль)
6. - 30 - колич. секторов в схеме "Цикл Метона"
7. - 30 - колич. секторов в схеме Дж. Бруно
8. - 30 - колич. градусов приход. на каждое зодиакальное созвездие
9. - 30 - колич. ребер додекаэдра (и колич. ребер икосаэдра)
Получается, что треугольник Пифагра (5-12-13) своими периметром (30) и площадью (тоже - 30) позиционирует два Платоновых тела (количество ребер) - додекаэдр и икосаэдр.
Засим - проект "Водовзводная башня" - образчик высочайшего взлета неопифагоризма Здравствуйте!
Диаметр окружности длиной в Короткий Фарлонг (242 МЯ - мегалитических ярдов) - 77 МЯ....
Сарос - временной период - представляет не только число "223" (число 223 синодических месяцев Луны), но и число "242" (число драконических месяцев)...
Длина окружности Кругов в Марлборо-Даунс (КМД) - 300 коротких фарлонгов (КФ).
По Д. Фарлонгу КФ равен 242 Мегалитических ярда (МЯ).
Отсюда диаметр КМД равен 300*77 МЯ.
Интересно, что один из Модулей Пантеона (высота его цилиндра) равен 77 римских локтей. Внутренний периметр Пантеона представляет собой окружность длиной в 4 таких модуля - длиной в 308 римских локтей...
Сие позволяет допустить возможность и иных (античных) представлений сароса.
Кроме того про сарос (касательно палеолита) см. работы В. Ларичева.
cтраницы обсуждения
1 2 3 4 5 6 7 8 9 10 >>

 (с) 2002-2024 СибДИЗАЙН.ру
(с) 2002-2024 СибДИЗАЙН.ру
|

|